Recent advancements in diffusion models have been effective in learning data priors for solving inverse problems. They leverage diffusion sampling steps for inducing a data prior while using a measurement guidance gradient at each step to impose data consistency. For general inverse problems, approximations are needed when an unconditionally trained diffusion model is used since the measurement likelihood is intractable, leading to inaccurate posterior sampling. In other words, due to their approximations, these methods fail to preserve the generation process on the data manifold defined by the diffusion prior, leading to artifacts in applications such as image restoration. To enhance the performance and robustness of diffusion models in solving inverse problems, we propose Diffusion State-Guided Projected Gradient (DiffStateGrad), which projects the measurement gradient onto a subspace that is a low-rank approximation of an intermediate state of the diffusion process. DiffStateGrad, as a module, can be added to a wide range of diffusion-based inverse solvers to improve the preservation of the diffusion process on the prior manifold and filter out artifact-inducing components. We highlight that DiffStateGrad improves the robustness of diffusion models in terms of the choice of measurement guidance step size and noise while improving the worstcase performance. Finally, we demonstrate that DiffStateGrad improves upon the state-of-the-art on linear and nonlinear image restoration inverse problems.
ICLR 2025
Inverse problems are ubiquitous in science and engineering, playing a crucial role in simulation-based scientific discovery and real-world applications. These problems arise in fields ranging from medical imaging and remote sensing to astrophysics and computational neuroscience. At their core, inverse problems aim to recover an unknown signal from noisy observations, where the measurement process may be incomplete or degraded.
Traditional approaches have relied on sparse priors, providing theoretical guarantees for unique data recovery. More recent approaches leverage information directly from data, with state-of-the-art techniques employing generative diffusion models. Despite their impressive capabilities, diffusion models face significant challenges in solving inverse problems. The primary difficulty stems from the intractability of the posterior distribution when using unconditionally trained models. These approximations often lead to inaccurate sampling and artifacts in reconstructed data. Furthermore, current diffusion-based approaches lack robustness to parameters such as gradient step size and measurement noise, limiting their practical utility in real-world applications.
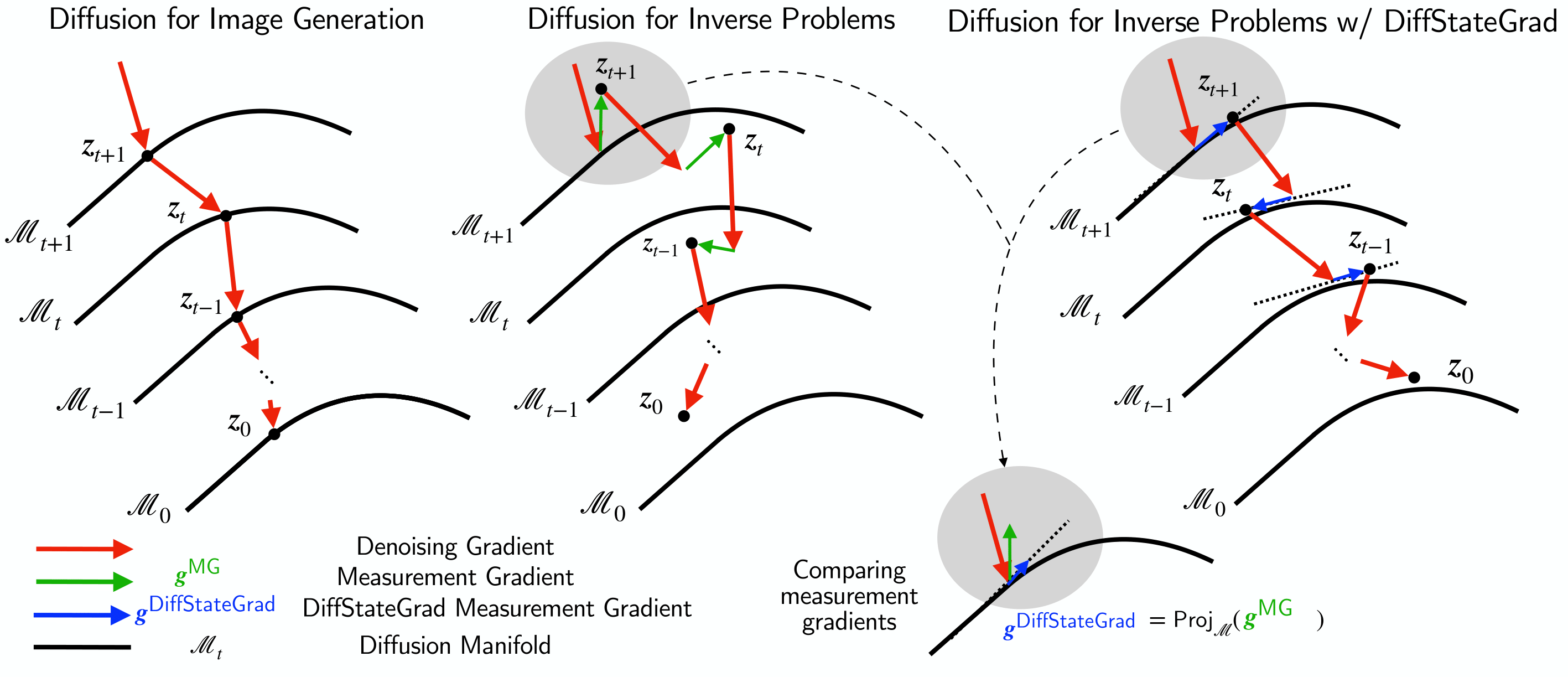
DiffStateGrad projects the measurement gradient onto a subspace defined to capture statistics of the diffusion state at time t on which the gradient guidance is applied. This helps the process stay closer to the data manifold during the diffusion process, resulting in better posterior sampling. Without such projection, the measurement gradient pushes the process off the data manifold.
We propose a Diffusion State-Guided Projected Gradient (DiffStateGrad) to address the challenge of staying on the data manifold in solving inverse problems. We focus on gradient-based measurement guidance approaches that use the measurement as guidance to move the intermediate diffusion state toward high-probability regions of the posterior. DiffStateGrad projects the measurement guidance gradient onto a low-rank subspace, capturing the data statistics of the learned prior. We define a projection step to preserve the measurement gradient on the tangent space of the state manifold. We achieve this projection by performing singular value decomposition (SVD) on the diffusion state of an image to which guidance is applied and use the highest contributing singular vectors as our projection matrix.
Our key contributions include:
• Showing that the crucial factor is the choice of the subspace, not just its low-rank nature
• Theoretically proving how DiffStateGrad helps samples remain on or close to the manifold, improving reconstruction quality
• Increasing the robustness of diffusion models to measurement guidance gradient step size and measurement noise, with dramatic improvements in metrics across various tasks
• Improving metrics significantly - for example, DiffStateGrad reduces the LPIPS of PSLD from 0.463 to 0.165 on random inpainting with large step sizes
• Empirically demonstrating that DiffStateGrad significantly improves worst-case performance, reducing the failure rate from 26% to 4% on phase retrieval tasks
• Consistently showing lower standard deviation than state-of-the-art methods
.png)
DiffStateGrad improves worst-case performance.
DiffStateGrad significantly improves the robustness of diffusion models to various factors. Our experiments show that while conventional methods deteriorate when measurement gradient step size increases, DiffStateGrad maintains high performance across a wide range of step sizes. Similarly, when faced with increasing measurement noise, DiffStateGrad exhibits superior resilience compared to standard methods, which experience substantial performance degradation.
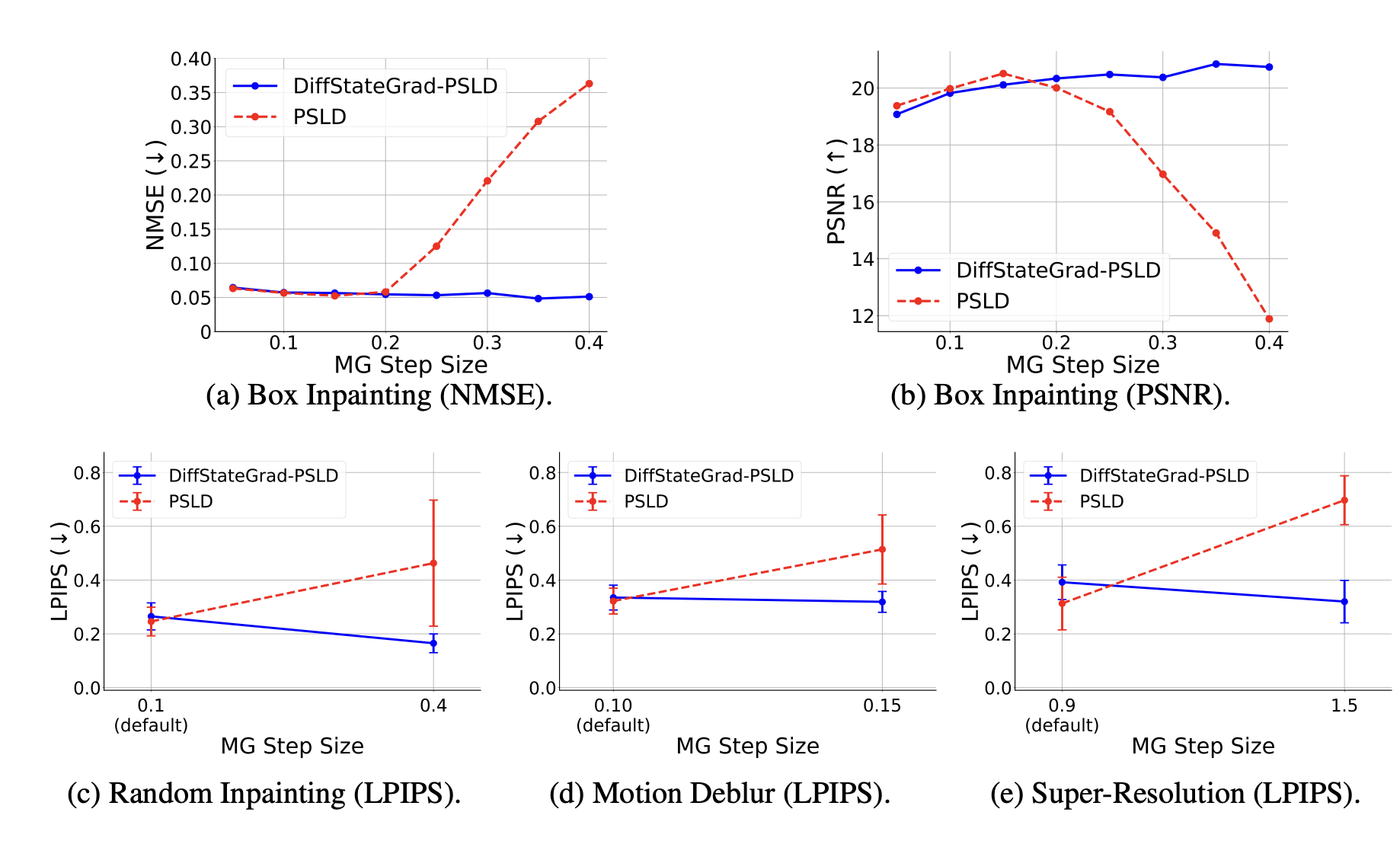
DiffStateGrad improves robustness to measurement gradient (MG) step size.
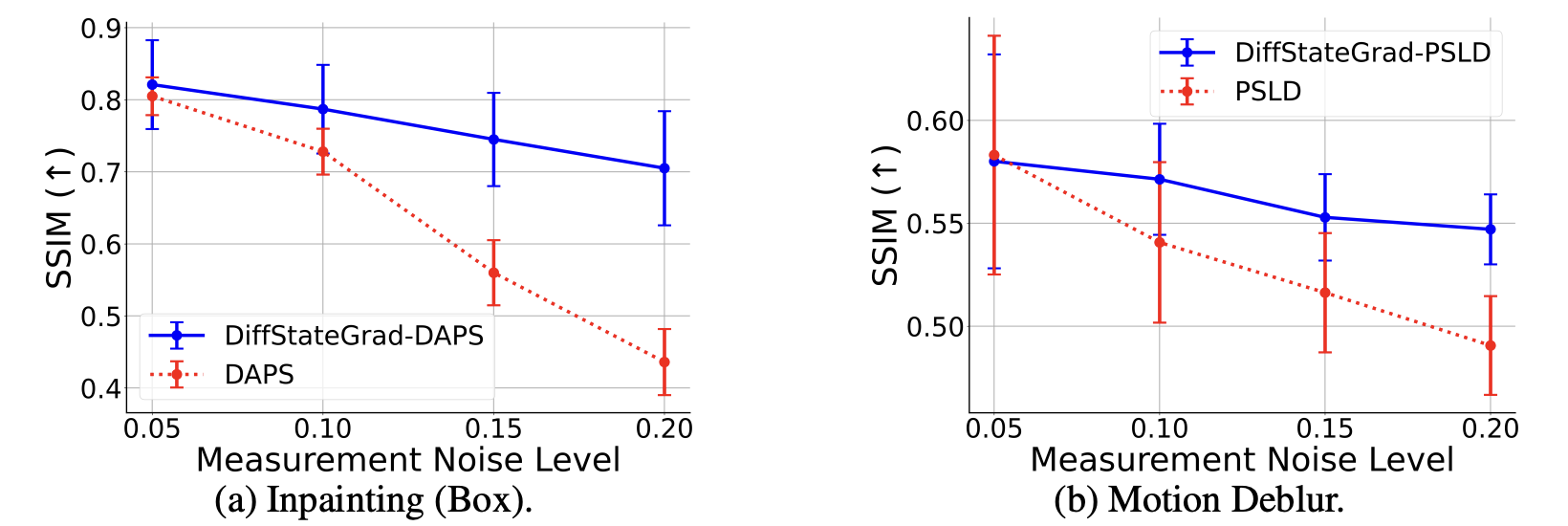
DiffStateGrad improves robustness to measurement noise.
Our quantitative and qualitative results demonstrate substantial improvement in performance across a variety of linear and nonlinear tasks. DiffStateGrad enhances both pixel-based and latent solvers, with particularly impressive gains in challenging tasks like phase retrieval and high dynamic range reconstruction. For example, when applied to ReSample for phase retrieval, DiffStateGrad improves PSNR from 27.61 to 31.19 while reducing standard deviation from 8.07 to 4.33, indicating both better and more consistent performance.
DiffStateGrad removes artifacts and reduces failure cases, producing more reliable reconstructions.
.png)
DiffStateGrad produces consistent reconstructions in challenging non-linear tasks such as phase retrieval.
If you find our work interesting, please consider citing
@inproceedings{zirvi2025diffusion,
title={Diffusion State-Guided Projected Gradient for Inverse Problems},
author={Rayhan Zirvi and Bahareh Tolooshams and Anima Anandkumar},
booktitle={The Thirteenth International Conference on Learning Representations},
year={2025}
}